Illustrative Example:
Consider the following data set:
2.1, 2.3, 2.6, 2.1, 1.9, 2.2, 1.8, 3.8
The values are centered fairly evenly around 2.3, except for the
final value of 3.8. The question is, what is the chance that this
large value occurred by random chance, and is it a valid measurement
of the system we’re interested in? Or, or is it a spurious
result from a different system entirely? We can look at the probability
distribution for this set of data, which has a
mean of 2.35 and a
standard deviation of 0.635.
The probability distribution is shown below:
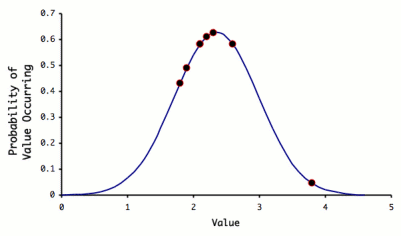
Probability distribution for a system with μ=2.35 and
σ=0.635 (solid line), with the experimental values from
the above dataset shown as discrete points.
The probability of each value occurring refers to the relative frequency
with which each value occurs for a large (n→∞)
number of replicate measurements. As you can see, all the measurement
values have a fairly high probability of occurring with the exception
of 3.8, which would only occur with a probability of less than 0.05,
or 5% of the time (1 time in 20).
In other words, if you made many measurements of a system with mean 2.35 and
standard deviation 0.635, there is a 5% chance that you would get a result
near 3.8. Getting one or two results in the neighbourhood of 3.8 is
therefore not completely unlikely, but a large number of results around
3.8 would be highly unlikely.
If were you to observe many values around 3.8, it is much more likely that
the system changed while you where working, so that effectively you are
measuring a different system to the one you started with. In this case,
you could be 95% confident that the value of 3.8 is from a different system.
We call this a 95% confidence level, or 95% CL.

